Collision Detection

• For any two objects that are close enough, we need to detect if their surfaces intersect.
• We can prevent an object in the scene from moving forward if there is an intersection.
• If the objects are a collection of polygons, we need to compute the possible intersection of each polygon from one object with all polygons from the other.
• This is usually very time consuming.

Collision Meshes

• Many game engines will allow (or require) the user to define a collision mesh for any object in the scene for which we need to detect the collision with other objects.
• The collision meshes are not displayed. They are only used to compute intersections with other objects instead of the polygons composing the object.
• The collision meshes are defined to make the computation easier: boxes, spheres, cylinders. The fastest test is the one you don't do.

Coplanar Polygons Intersection

• Two coplanar polygons intersect if at least one vertex from one is inside the other polygon, or if at least two edges of the polygons intersect.
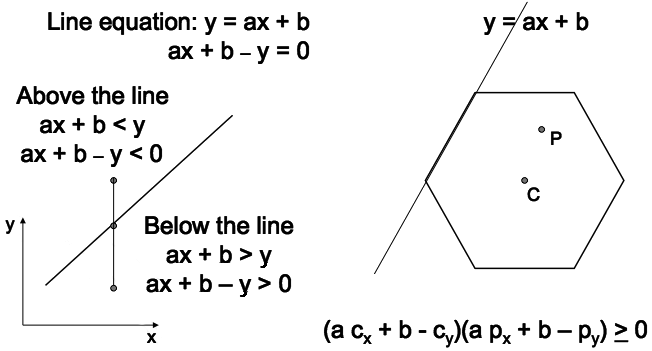
• Suppose we have a convex polygon and a point inside the polygon (center). Then an arbitrary point is inside the polygon if it's on the same side as the center of all the lines composing the polygon.
• Each polygon can be decomposed in triangles and the intersection computed for each couple of triangles.

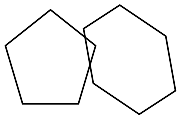
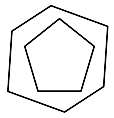
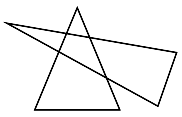
Polygons Intersections

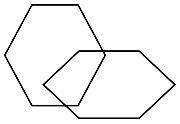
Both polygons have vertices inside the other	Only one polygon has a vertex inside the other
No edge crossing	No vertex is inside any of the polygons

Inside a Polygon

Edges Intersection

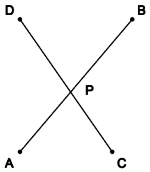
Equations of the two lines:
(P_x - A_x)/(B_x - A_x) = (P_y - A_y)/(B_y - A_y)
(P_x - C_x)/(D_x - C_x) = (P_y - C_y)/(D_y - C_y)
By solving these we find P.

P must be between A and B and between C and D on the lines:
(P_x - A_x)(P_x - B_x) < 0
(P_x - C_x)(P_x - D_x) < 0
Only one coordinate needs to be checked because the points are colinear.

Both the vertex check and the edge check are O(n²), where n is the number of vertices in the highest polygon.

Two-Phase Algorithms

• In a scene with m objects, the algorithm must compute O(m²) intersection of pairs of objects.
• A two-phase algorithm eliminates most of the collision computations based on bounding boxes/spheres, etc. This is called the broad phase.
• For moving objects, one can compute the bounding box of the entire movement in the unit of time.
• To eliminate some of the intersection, a hierarchical tiling of the space can be used (quad tree), or a coordinate sorting.
• This phase can be made almost O(m) (linear).

Swept Volume for a Moving Object

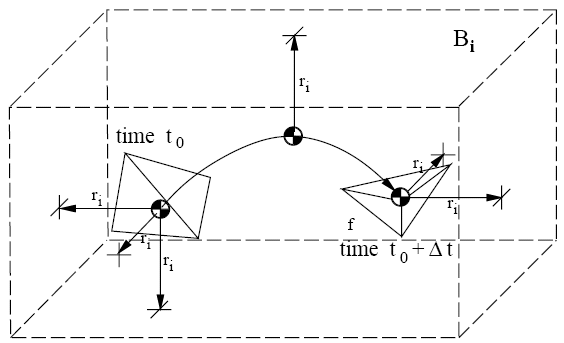
From B. Mirtich (1997): Efficient Algorithms for Two-Phase Collision Detection, Technical Report TR-97-23, Mitsubishi Electric Information Technology Center America.

Coordinate Sorting

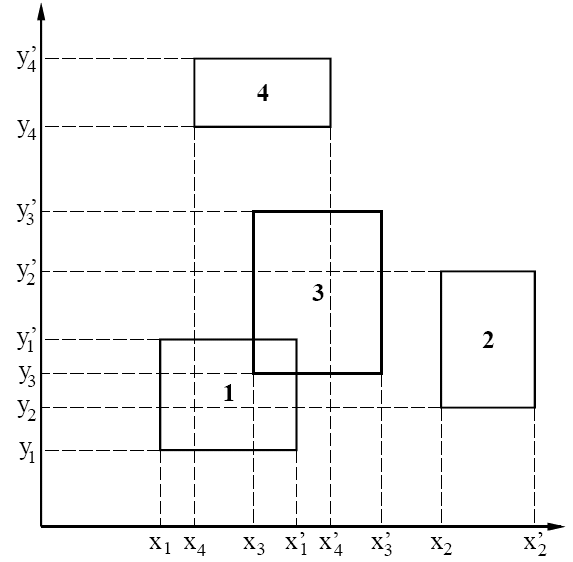
A hash table can be used to improve the sorting.

Narrow Phase Collision

• Analyzes more carefully pairs of coordinates that are not culled by the broad phase.
• Some of them would return the distance between non-intersecting objects that can be used in movement planning.
• Some optimizations

Lin-Canny Algorithm

• Lin-Canny closest features algorithm determines the closest faces / edges / vertices between two polyhedral objects.
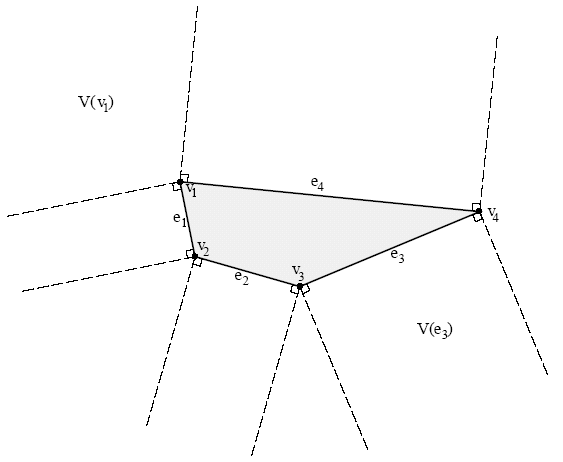
• It uses the Voronoi regions for each feature (see next slide). Let F be a feature and V(F) its Voronoi region.
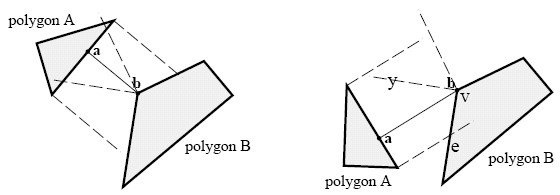
• If A and B are the closest features of two polygons, and a and b the closest points in each feature, then a is in V(B) and b is in V(A).
• The algorithm iteratively reduces the current closest features.
• Alternatives exist that consider the coherence of the scene over time.

Voronoi Regions

Lin-Canny Algorithm

Other Algorithms

• V-Clip Algorithm - an improvement of the Lin-Canny algorithm, also using the Voronoi regions.
• GJK (Gilbert, Johnson, Keerthi) - simplex-based algorithm. It considers the polyhedra as clouds of points and computes a simplex (point, bounded line, triangle, or tetrahedron) as a bounding region of the Minkowski difference polyhedron (or TCSO).
• The TCSO (transitional configuration space obstacle) is a collection of vectors obtained from the difference of points from the two polyhedra.
  TCSO = {b-a | a is in A and b is in B}.
• Public libraries for collision-detection are available, like I-Collide, V-Collide, QHull, ColDet.

3D Intersections

• Plane equation: ax + by + cz + d = 0
• The two sides of the plane are defined by
  ax + by + cz + d < 0
  ax + by + cz + d > 0
• Two points P and Q are on different sides of the plane if
  (a P_x + b P_y + c P_z + d) * (a Q_x + b Q_y + c Q_z + d) < 0

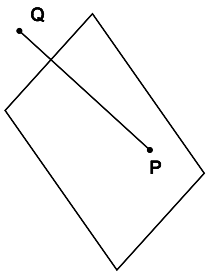
Movement through a Polygon

• By moving an object by a certain vector in the scene, the object may go to the other side of the polygon.
• In this case we have to determine if the line segment between the two object positions crosses the polygon.
• We must compute the intersection point of the line and the plane, then verify that it's inside the line segment and inside the polygon.

Crossing a Polygon

• First we must check that the origin O and the destination D are on different sides of the plane.
• Plane: ax + by + cz + d = 0
• Line segment:
  D = O + (t L_x, t L_y, t L_z)
  where L is the direction vector
• P the intersection point is defined as satisfying both the plane and the line segment equations.
• Then we must check that P is inside the polygon based on the equations described before.

Non-Coplanar Polygons

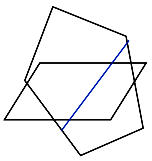
• Compute the intersection line based on the plane equations.
• Check if the line intersects any of the polygons.
• If it intersects both, then a point on this line must be on an edge of one polygon and at the same time inside the other one.

Box - Sphere

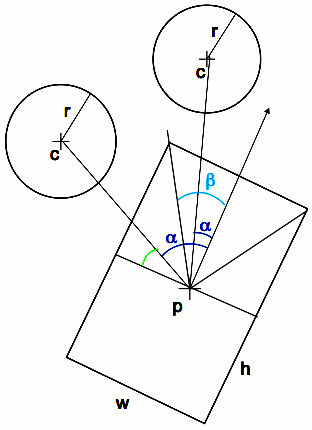
• Maximum distance at which we can still have an intersection
  max = r + sqrt(w² + h²)/2
  If d(c, p) > max, we don't need to check for collision.
• The collision threshold thr can be computed as:
  If alpha < beta:
     thr = r + (h/2) cos alpha
  else
     thr = r + (w/2) / cos (90-alpha) = r + (w/2) / sin alpha
• Linearizing the computation to avoid the sin/cos.
• Let dg = sqrt(w²+h²)/2
• If alpha < beta:
     thr = r + h/2 + (alpha/beta) (dg-h/2)
  else
     thr = r +w/2 + ((alpha-beta)/(90-beta) (dg - w/2)
• Note: the intersection is computed in the XZ plane because both objects are bound to the ground (terrain).

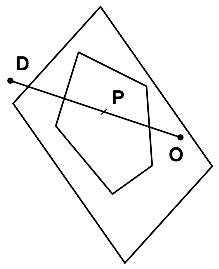
Moving Past a Sphere

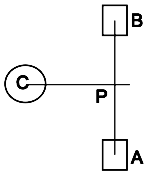
• When the sled moves from A to B in one frame, it may collide with a snowball on the way.
• We have to project the ball's center on the movement line, and if the distance to the line is less than the max and P is between A and B, then we must compute the collision between the objects at the point P.
• The distance between C and a line of equation ax + bz + c = 0 is
  (a c_x + b c_z + d)/sqrt(a²+b²)

Motion and Collision

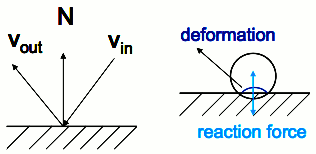
• When an object hits a surface with a certain velocity, it may bounce from the surface depending on the object elasticity.
• A perfectly elastic object bounces from a surface with a speed equal to its original speed, but in a direction symmetric with respect to the surface normal.

Imperfect Bouncing

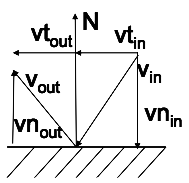
• If the object is not perfectly elastic, then part of the energy resulting from the collision is absorbed.
• The speed can be decomposed in a vector tangent to the surface and one normal to the surface.
• The tangent component doesn't change.
• The normal component is partially absorbed by a factor e depending on the two surfaces.
• v_out = vt_out + vn_out = vt_in + e vn_in
• If |N|=1, then vn_in = N v_in (scalar product)
• vt_in = v_in - vn_in