C481 B581 Computer Graphics
Dana Vrajitoru
OpenGL
Portable library for fast, interactive, 2D, and 3D computer graphics.
Some advantages:
-
Open, vendor-neutral, multiplatform graphics standard.
-
Supported and used by the industry.
-
Stable, reliable, and portable.
-
Runs on the major operating systems: Unix / Linux, Windows, MacOS and
on some other platforms like the iPod.
A collection of data types and functions, also called commands.
Components of OpenGL:
-
Basic library: GL.
-
GLU - graphics utility library - code for some higher level objects like
spheres
-
GLUT Graphics Utility Toolkit - user interface.
GLUT Introduction
A relatively simple GUI library.
- The interface objects are hidden from the user. All we can get is
some "id" associated with graphical objects.
- All communication with the interface is done through some simple
function calls.
- It only allows for pop-up menus.
- One or two windows.
Some GLUT functions
| glutInit(&argc, argv)
|
To be called in the beginning of the program.
|
|
glutCreateWindow(title)
| Creates the application window. All GL command will be displayed on this
window.
|
|
glutDisplayFunc(function)
|
To be called for every update type of event.
|
|
glutIdleFunc(function)
|
Called repeatedly if the user doesn't input anything (animation).
|
|
glutMainLoop()
|
To be called to launch the application (GUI).
|
|
glutMouseFunc(function)
|
Callback function for any mouse event.
|
Geometrical commands
glBegin, glEnd - delimit the vertices of a primitive or of a group of similar
primitives
void glBegin( GLenum mode );
void glEnd( void );
Between glBegin and glEnd, a list of vertex primitives, for example
void glVertex3f (GLfloat x, GLfloat y, GLfloat z );
Consider the list pi = glVertex(xi, yi,
zi); 1 < i < n
.
Geometrical mode:
| GL_POINTS |
Each pi is drawn as a point. |
| GL_LINES |
Each (p2i, p2i+1) makes a line segment. |
| GL_LINE_STRIP |
Each (pi, pi+1) makes a line segment. |
| GL_LINE_LOOP |
Similar to line strip, plus (pn, p1) also makes
a line segment. |
| GL_TRIANGLES |
Each (p3i, p3i+1, p3i+2) makes a triangle. |
| GL_TRIANGLE_STRIP |
Each (pi, pi+1, pi+2) makes a triangle. |
| GL_TRIANGLE_FAN |
Each (pi, pi+1), i>0, makes a triangle with p1. |
| GL_QUADS |
Each (p4i, p4i+1, p4i+2, p4i+3)
makes a quadrilateral. |
| GL_QUAD_STRIP |
Each (p2i, p2i+1), (p2i+3, p2i+2)
makes a line quadrilateral. |
| GL_POLYGON. |
A single polygon with n sides. |
Color in OpenGL
- Defined by R, G, B in the range 0.0 to 1.0.
- glColor3f(r, g, b);
- options: d, f, b, i, s, u-unsigned, v-vector.
- To clear the window with a given color:
- glClearColor(r, g, b, alpha);
- alpha = 1.0 for opaque, alpha = 0.0 for completely transparent.
Interpolating the Color
-
A glColor command defines the color to be applied to all geometrical commands
that follow it.
-
A new glColor command has the effect of interpolating the color between
the previously defined color and the new one for all the geometrical commands
in between.
Display Lists
- Def. A display list is a compiled group of OpenGL commands
that have been stored under a unique identity (integer) for later
execution.
- When a display list is invoked, the commands in it are executed in
the order in which they were issued.
- Display lists can be drawn fast and easily by one function call.
- Useful for objects that will be drawn more than once.
- Creating a display list (the second parameter can also be
GL_COMPILE_AND_EXECUTE):
glNewList(id, mode); // Starts a new display list
any GL/GLU commands in between
glEndList();
where mode can be
| GL_COMPILE |
The commands in the list will not be executed as they are stored
in the display list. |
| GL_COMPILE_AND_EXECUTE |
The commands will be executed as they are stored in the display list. |
- Drawing the display list:
glCallList(id);
Matrix Mode in OpenGL
There are 3 matrices in OpenGL,
-
for the objects in the scene (model view),
-
for the camera (point of view or projection),
-
for the texture.
Only one of them is active at any time.
All of the transformations are defined as matrices that are multiplied
with the active matrix.
See page 68 from the textbook.
Matrix Operations
-
Switching the matrix mode:
glMatrixMode(GL_PROJECTION);
glMatrixMode(GL_MODELVIEW); // default
glMatrixMode(GL_TEXTURE);
-
Setting a matrix to the identity:
glLoadIdentity();
-
Loading a particular matrix:
glFloat m[] = {1.0, 0.0, ... }; // 16 elem.
glLoadMatrixf(m); // f or d
-
Multiply the active matrix by a given matrix
glMultMatrixf(m); // f or d
The matrix stack
-
The 3 matrices are organized in a stack. One can push the active matrix
in the stack, then pop it out of the stack again.
glPushMatrix(); // save
glPopMatrix(); // restore
Example: Translate (obj1 Rotate (obj2) obj3) obj4
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glPushMatrix();
glTranslatef(tx, ty, tz);
obj1;
glPushMatrix();
glRotatef(...);
obj2;
glPopMatrix();
obj3;
glPopMatrix();
obj4;
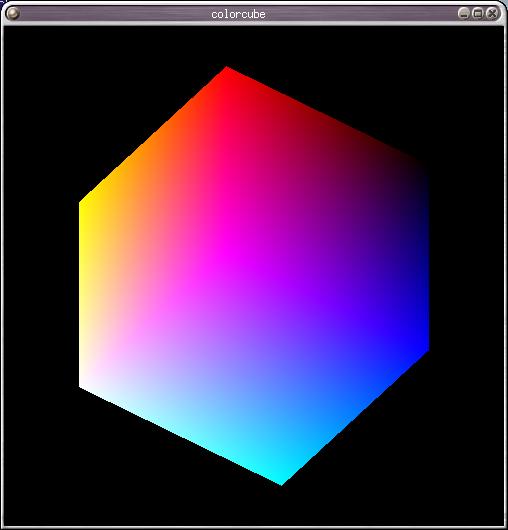
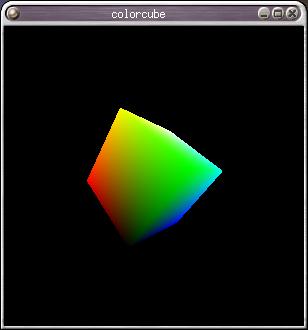
Case Study: the Spinning Cube
Programs: cube.c, cubeview.c from the textbook CD.
Goal: define a cube of edge=2, with the center in the
origin.
-
cube.c - parallel projection
-
cubeview.c - perspective projection
- cube1.cc -
cube.c, modified to spin slowly
Camera location and orientation (textbook, page 234):
gluLookAt(eyex, eyey, eyez, atx, aty, atz, upx, upy, upz);
Changing the Point of View
-
In parallel projection: call the glOrtho function again (see function myReshape).
-
In perspective projection: either by calling the gluLookAt plus the glFrustum
or gluPerspective
 |
 |
| parallel projection (cube.c) |
perspective projection (cubeview.c) |
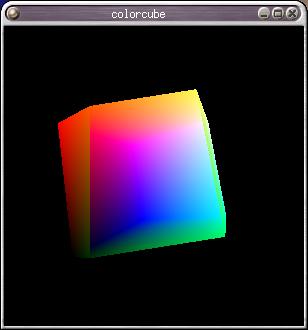 |
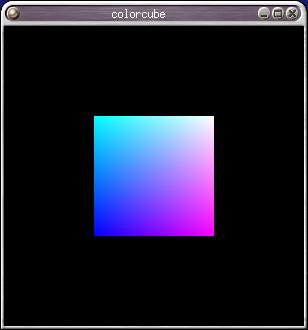 |
| perspective, the close plane cuts the cube |
persective centered front view |







