C481 B581 Computer Graphics
Dana Vrajitoru
Hidden Surfaces
Determine which parts of the scene are seen by the viewer (camera)
and which are not. Allows the user to create a mental 3D spatial representation
of the 2D image.
For an object, determine the point of view and orientation
For several objects, determine their position with respect to each other:
Depth Comparison
If two points P1(x1, y1, z1)
and P2(x2, y2, z2) result in
the same projection, compare the distance between each of them and
-
the projection plane for the parallel projection
-
the projection center for the perspective projection.
If we project on the 0xy plane, we just have to compare z1 and
z2: the point with smaller depth is visible.
Detection algorithms:
-
object-space methods
-
image-space methods.

General Idea
- We consider that the user's eye is on the projection plane for the
parallel projection.
- For the perspective projection, we use the projection matrix to
deform the scene first.
- The projected image is then be obtained with a parallel
projection.
- Thus, we only need to solve the problem for the parallel
projection.
Back-Face Detection
- An object-space method.
- Consider the normal to a surface N and the view vector V. If angle(V,
N) < 90, then the face is a back face.
- In the case where the projection is on the (0xy) plane, if the z
component of the normal, Nz > 0, then the face is hidden.
- Only works if the object is closed. Can be used to preprocess the
scene.
Z-Buffer Algorithm
- An image-space method.
- For each pixel (x,y) in the projection plane, keep the value of
the closest z value that has been drawn on it.
- 1. Initialize the projection area to a background color.
- 2. Initialize the z-buffer to a maximal number (back clipping plane).
- 3. Scan-convert one polygon (triangle) at a time. For each converted
point, compare its z with the value stored for that pixel in the z-buffer.
If the new value is smaller, draw the point.
A-Buffer Algorithm
- Similar to the z-buffer method, only considers transparency.
- For each pixel record all the scan-converted points, with depth
and opacity parameter.
- Compute the color of the pixel based on all this information.

- color(P) = a2 * color(P2) + (1-a2) (a1*color(P1) + (1-a1) (a3*color(P3)
+ (1-a3)*background))
= 0.8 c2 + 0.2 (0.3 c1 + 0.7 (0.5 c3 + 0.5 bcgr)
= 0.8 c2 + 0.06 c1 + 0.065 c3 + 0.065 bcgr
Hidden Surfaces in OpenGL
- Enable the z-buffer:
glEnable(GL_DEPTH_TEST);
- Disable the z-buffer:
glDisable(GL_DEPTH_TEST);
- Clear the z-buffer:
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
Painter's Algorithm
- Suppose that we have a set of polygons or other objects sorted by
the distance to the view plane.
- Some of them might overlap, in which case the one closer to the
plane needs to appear in front.
- We can simply "draw" or render them in depth order starting from
the farthest one (back to front). The color of a polygon that is
render at any step replaces any other color that might have been there
before.
- It works very well when all the objects are parallel to the view
plane, like in 2D with a z component or 2.5D graphics.
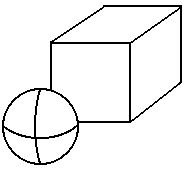
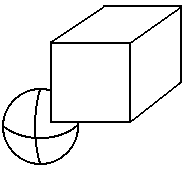
Example

Depth Sorting
- Object-based method for 3D hidden surface removal, a variation of
the painter's algorithm.
- In 3D we don't have a single z coordinate for each polygon, we
have an interval [zmin, zmax] called z extent.
- If the z extents of two polygons don't intersect we can render
them back to front.
- If their z extents intersect but their x extents or y extent don't
intersect, we can paint them in any order.
- Otherwise in the worst case we have to split some polygons by the
intersection lines and render them separately.