Processor: A CPU, an independent physical computing unit in a computer. A computer must have at least one CPU but it can have more than one.
Process: a sequential set of instructions that is being executed by a CPU.
Program: one or more processes that work together to perform a task.
Sequential program: one that is composed of only one process. It is obviously executed on a single CPU.
Parallel program: a program made of several processes that are executed by one or more CPUs. The CPUs may be on one or more computers.
Concurrent program: one that is composed of two or more processes sharing some resources. Example: an operating system.
Distributed program: a parallel program that is executed on several CPUs that exist physically on several computers (a network).
Parallel Programming Models
Criteria:
SIMD - Single Instruction stream Multiple Data
stream.
All of the processes execute exactly the same code. Each process
has its own memory that other can't have access to. Any information
that needs to be shared is exchanged by message passing. Best known
example: MPI (Message Passing Interface).
MIMD - Multiple Instruction Multiple Data
Each process
can execute a different set of instructions. Usually, some of them are
allowed to execute the same set of instructions. Each process has its
own memory that other can't have access to. Any information that needs
to be shared is exchanged by message passing. Best known example: PVM
(Portable Virtual Machine).
SISD - Single Instruction Single Data
All of the processes execute code taken from the same program, but
either different parts of it, or based on different sets of
parameters. The processes share the memory. Best known example:
threads, pthreads (POSIX threads).
MISD - Multiple Instruction Single Data
It does not exist in theory. When two programs running independently
access each other's memory, it can create runtime errors. It's what a
good operating system is supposed to avoid.
Communication
Synchronization
Auto-parallelizing compilers: MPISpro, KAP
Parallelism Terms
An example
Computing the integral of a function in a given interval.
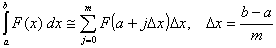
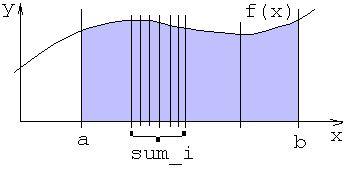
If n is the number of processes, and we label them from 0 to n-1,
for (each process i) // in parallel sum_i = Integral(a+i*(b-a)/n, a+(i+1)*(b-a)/n, F); integral = 0; for (i=0; i<n; i++) // in sequence integral = integral + sum_i;
IVP (Initial Value Problem) solver.
An n-dimensional curve s(t), 0 <= t <= c, defined by:
s(0) known,
s'(t) = F(s(t))
s(t+Dt) = s(t) + s'(t)Dt
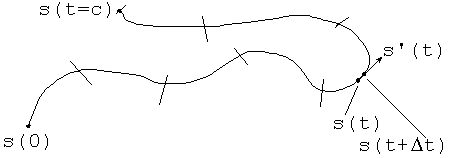
Example:
F = const - a line segment
A circle:
x'(t) = -y(t)
x(t) = cos t
y'(t) = x(t)
y(t) = sin t
0 <= t <= 2p
Let's say that we want to solve this problem with p processes.
Unreasonable problem division: if we divide the interval [0, c] in p intervals, and we try to compute the curve by a separate process on each interval, it doesn't work. We need the starting point for each interval that must be computed based on the previous point. So each process would have to wait for the previous one to finish the computations before it can start working. The result is worse than the sequential program.
Reasonable problem division: if s has more than one dimension, the derivate in each dimension does not depend on the others, so it can be computed independently. Thus, we split the computation of each new point among processes. In this case, p <= n, the number of dimensions of s.
For the circle, we can only use 2 processes.
A very general model in which a particular process organizes all of the others.
Most parallel programs follow it implicitly or explicitly.
The master is in charge of input-output operations, collects the data from the others, synchronizes all of them, makes decisions.
Deadlock
Situation where one or more processes are waiting for information from other processes in a loop.
Famine
Situation in which one or more processes are waiting for some resources to continue their execution and never get them, but the whole program goes on nonetheless.
The Problem of the Dining Philosophers
The problem was invented by E. W. Dijkstra and is often used to illustrate the problem of concurrent threads competing for limited resources. The original problem involves five philosophers, but versions with different numbers also exist.
Five philosophers sit around a table, a bowl of rice in front of each of them and a fork (or chopstick) between each of them. They can either eat or meditate. In order to eat, they need to acquire the forks or chopsticks on both sides (left and right). If they can't eat, they meditate. One can assume that any philosopher will only eat for a limited amount of time, and then they will put the forks down and start meditating. The problem is to organize their activities such that none of them is starving.

Solution 1
for each philosopher i
while true
if (fork(i).Try_to_reserve()) {
while (!fork((i-1)%5).Try_to_reserve())
Meditate();
Eat();
fork(i).Release();
fork((i-1)%5).Release();
}
else
Meditate();
Deadlock situation: if each philosopher reserves the fork to its right in the beginning, they are all blocked in waiting for the left fork.
Solution 2
for each philosopher i
while true
if (fork(i).Try_to_reserve()) {
if (fork((i-1)%5).Try_to_reserve()){
Eat();
fork(i).Release();
fork((i-1)%5).Release(); }
else {
fork(i).Release();
Meditate(); }}
else
Meditate();
Famine situation: It can happen that a philosopher reserves a fork, tries for the second one which is taken, releases the first, and so on for ever without managing to actually eat.
Speedup - the gain in computation time.
Comparing the parallel algorithm with the best sequential algorithm that can solve the problem.
If n is the size of the problem and p the number of processes, then we have
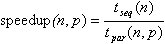
where tseq(n) is the execution time on a similar processor of the best of the known sequential algorithms, and tpar(n,p) is the execution time of the parallel program for p processes.
Often the speedup is expressed as percentage.
A speedup of 100% means no improvement.
The maximum possible speedup is p*100%. For example, for 4 processes, that would be 400%.
Some parts of the program can only be executed by 1 process at a time (output), and cannot be divided among the processes.
Amdahl's law. If f is the fraction of the sequential program that cannot be divided, then the maximum possible speedup is
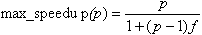
Efficiency:
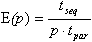
The lower bound for the efficiency is 1. Lower values for the efficiency are better.
Cost:
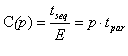
Load balancing:
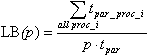
A measure of how much each process is actually used. The maximum possible is 1.
Scalability: describes algorithms that can accommodate increased data with limited increase in computational time. Many problems are relatively easy to solve on small amounts of data but become very difficult for large amounts (NP-complete problems). Ideally a program is scalable if its efficiency does not depend on the number of processes p.