Dana Vrajitoru
B424 Parallel and Distributed Programming
Exploratory and Speculative Decomposition
Exploratory Decomposition
- Example: looking for the best move in a game.
- Simple case: generate all possible configurations from the
starting position.
- Send each of the configurations to a child process.
- Each process will look for possible best moves for the opponent
recursively eventually using more processes.
- When it finds the result, it sends it back to the parent. The
parent selects the best move from all of the results received from the
child (eventually the worst move for the opponent).
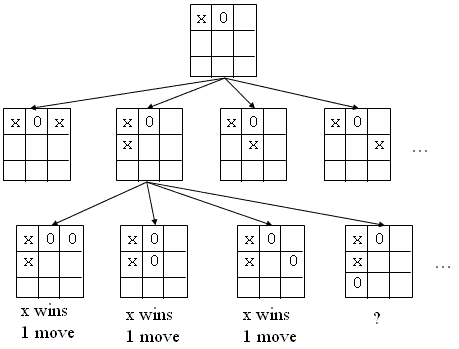
Figure: Tic Tac Toe game,
exploratory decomposition
Speculative Decomposition
- Consider the situation of a switch statement in a program. Usually
we wait to know the value of the expression the switch is based on and
execute only the case corresponding to it.
- In speculative decomposition we execute some or all of the cases
in advance.
- When the value of the expression is know, we keep only the results
from the computation to be executed in that case.
- The gain in performance comes from anticipating the possible
computations.
| Sequential version
| Parallel version
|
compute expr;
switch (expr) {
case 1:
compute a1;
break;
case 2:
compute a2;
break;
case 3:
compute a3;
break;...
}
|
Slave(i)
{
compute ai;
Wait(request);
if (request)
Send(ai, 0);
}
Master()
{
compute expr;
swicth (expr) {
case 1:
Send(request, 1);
Receive(a1, i);
...
}
|
Example - TTT Game
- As before, we compute a tree of possible configurations with
estimation of performance for each of them.
- The difference with the exploratory decomposition is that we can
compute the possible states before the next move is performed.
- This way after 0 makes a move, we as the process in charge of that
particular state for the info on the best next move for x.
- The best move being computed in advance, it may take long to fire
up the program, but after that, playing can be very fast.
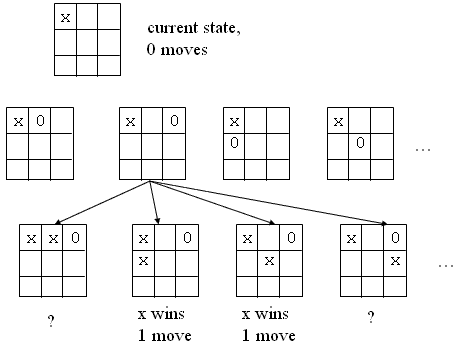
Figure: Tic Tac Toe game,
speculative decomposition
Discreet Event Simulation
Figure: Discreet event
simulation
Topological Sorting
- Suppose we have to perform a number of tasks, some of which depend on others, and we can only do one at a time.
- We can organize the tasks in a dependency graph.
- We must find an ordering of the tasks respecting the dependencies.
- Example: T1, T6, T3, T4, T5, T2.
The Problem
- The Topological Sorting Problem: Given a digraph G, find, if
possible, a non-repetitive listing of all its vertices in such an
order that for every pair of vertices x and y, if the edge (x, y) is
in the graph G, then x precedes y in the list.
- Any listing of the vertices with these properties is called a
topological ordering of the vertices, and finding such a listing is
called sorting the vertices into a topological order.
- If we number the vertices in the order in which they appear in
such a list, we say that we have a topological numbering of the
vertices.
- Note: If the graph contains a cycle, then it cannot be
topologically sorted.
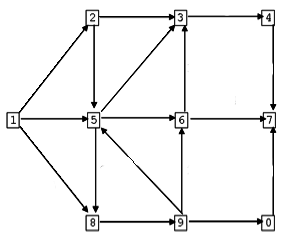
| 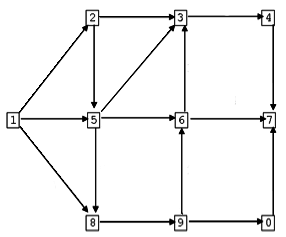
|
| A graph with no solution because of the cycle 5 6 9
5.
| A modification of the graph that makes the topological sorting
possible.
|
Sequential Version
boolean topologically_number (digraph G)
{
for (ever vertex v in G) {
visited[v] = false;
numbered[v] = false;
}
int topol_counter = number_of_vertices(G);
for (each vertex v in G)
if (!visited[v]) {
visited[v] = true;
if (!recursively_number(G, v, topol_counter))
return false;
}
return true;
}
boolean recursively_number (digraph G, int v, int & counter)
{
for (each w that can be reached from v) {
if (numbered[w]);
else if (visited[w]) // but not numbered
return false; // a cycle has been found
else {
visited[w] = true;
if (!recursively_number (G, w, counter))
return false;
}
}
vertex[v].topol_number = counter;
-- counter;
return true; // no cycles were detected
}
Parallel Outline
Process(id)
{
for all incoming "in"
Receive(dummy, in);
output id;
Perform_task(id);
for all outgoing "out"
Send(dummy, out);
}
Critical Path
- A path in the task dependency graph represents a sequence of tasks
that must be executed one after the other.
- The longest such path determines the shortest time in which the
program can be executed in parallel.
- The length of the longest path in a task dependency graph is
called the critical path length.
- The ratio of the total amount of work to the critical path length
is the average degree of concurrency.





