Dana Vrajitoru
C311 Programming Languages
Parsers
Parsing
- The most important part of any compiler.
- It relies on a context-free grammar.
- The input consists of code tokens.
- If n is the number of tokens in the code, then a typical parser
can compile a program in O(n3) time.
- Some particular grammars can be parsed in linear time: LL (left to
right, left-most derivation) and LR (left to right, right-most
derivation).
- LL parsers are top-down (predictive), while LR parsers are
bottom-up (constructive).
LL and LR Grammars
- An LL grammar is a grammar that can be recognized by an LL parser.
- Notation: LL(k) is an LL grammar for which the parser needs to
scan ahead k terminal symbols in the string to recognize. A similar
notation is used for LR(k).
- LL grammars are more general than LR. There exist grammars that
are not LL(k) for any given k.
Example
----- A: LL(1)--------
P -> ( P )
P -> R
R -> [ R ]
R -> e
----- B: non-LL--------
P -> ( P )
P -> P P
P -> e
----- C: LL(2)--------
R -> [ R ]
R -> [ ]
R -> P
P -> ( P )
P -> ( R )
P -> e
Languages Accepted by the Above Grammars
- A: (n [m ]m )n, where
n, m >= 0.
In other words, a sequence of parentheses followed by a sequence of
brackets, followed by the same number of closed brackets and
parantheses in reverse order.
Example: ( ( ( [ [ ] ] ) ) )
- B: a1 a2 a3 ... an where
ai is either ( or ),
for any i<n, count{ak = (, for k <= i} >=
count{ak = ), for k <= i}, (or the count of left parentheses
seen so far should be larger than or equal to the count of right
parenteses at any intermediate point in the string) and
count{ak = (, for k <= n} = count{ak = ), for k
<= n} (or the total count of left parentheses in the whole string
should be equal to the total count of right parenteses in the string).
In other words, a well formed sequence of parentheses where we never
close more parentheses than we have opened and where all opened
parentheses are closed by the end of the string.
Example: ( ( ( ) ) ( ) ) ( ( ) )
- C: a1 a2 a3 ... an
bn bn-1 ... b2 b1 where
n>=1 and
ai is either ( or [ , bi is either
) or ] and
if ai = (, then bi = ) otherwise
bi = ] (in other words, the parentheses and brackets should
be closed in reverse order than they were open).
In other words, a sequence of any combination of opened parentheses
and brackets followed by the same number of closed parentheses and
brackets in reverse order.
Example: [ ( ( [ ( [ ] ) ] ) ) ]
LL Parsing
- The parser starts with the root of the tree.
- At every step, it will try to expand the left-most non-terminal
active symbol (let's say S).
- The parser analyzes the next terminal symbol in the string (a) and
tries to make a prediction about the rule to be applied.
S =>a b c T
- It must match all terminal symbols to the left of the non-terminal
in the production rule (the string must contain a b c). The active
non-terminal symbol is replaced with the one to the right (T).
- The process stops when the parsed string is composed only of
terminal symbols.
More Examples LL Grammars
A Non-LL Grammar
This grammar is non-LL because to
choose between the two rules expanding UN one must find if there is a
preiod in the string or not. For that the parser must search forward
through all the digits. No matter what constant k we choose, it is
possible to have a number having more than k digits to the left of the
period, in which case the parser would fail to make a decision. So the
grammar is not LL(k) for any constant k, and so it is not an LL
grammar.
N => { + | - | e } UN
UN => UI . UI
UN => UI
UI => digit UI
UI => digit
LL - LR Parsing
- An example of LL(1) and LR(2) grammars to recognize a list of
identifiers in C++:
- LL:
id_list => id id_list_tail
id_list_tail => , id id_list_tail
id_list_tail=> ;
- LR:
id_list => id_list_prefix ;
id_list_prefix => id_list_prefix , id
id_list_prefix => id
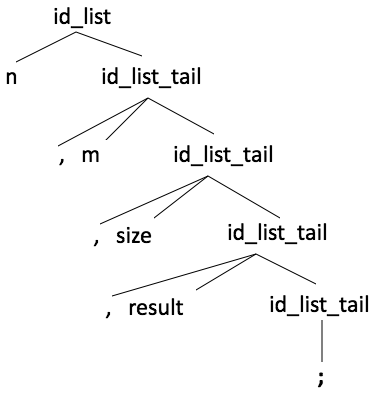
Example
- Parsing the following list: n, m, size, result;
- Starting with the id_list.
- Applying the first rule
id_list =>n id_list_tail
- Then we find a "," in the string which means that we apply the
second rule:
n id_list_tail =>n, m id_list_tail
- And so on until we find the ";" which prompts us to apply the
third rule:
n, m, size, result id_list_tail =>n, m, size, result;
Parse Tree
LR Parsing
- A LR parser is bottom-up.
- It starts by scanning the string and storing partially-completed
subtrees in a list.
- As soon as it notices that the right hand side of the list
corresponds to sequence to the right hand side of a rule, it replaces
that sequence with the non-terminal symbol to the left of the rule.
- The algorithm continues until we arrive at the starting
non-terminal, when the tree becomes complete.
Example Bottom-Up
- It starts from the left side and asks what subtreen could be part
of. Since it’s an id, it marks it as an IDLP(id(n)).
- Then it examines the next terminal, the comma, and asks what rule
could follow an IDLP with a comma. So it builds another
subtree IDLP(IDLP(id(n)) , id(m)).
- It continues this way adding things on top of the partial tree
that was constructed this far until the end of the input.
- It is called the right-most derivation because the root of the
tree starts with the terminals to the right. The processing of the
input string is still left to right.
Example LR
- Starting with the processing list
( n , m , size , result ; )
- We identify n as an id that can be a subtree of IDLP
(is_list_prefix):
( (IDLP n) , m , size , result ; )
- Then we notice that the combination of IDLP , m is the subtree of
another IDLP based on the second rule:
( (IDLP ( IDLP n) , m) , size , result ; )
- After repeating these steps the final result is:
(IDL (IDLP (IDLP (IDLP (IDLP n) , m) , size) , result) ; )
Parse Tree

Backus-Naur Notation
- BN notation used to describe the language Algol (1960).
- The Backus-Naur Form of a grammar is a convenient way to describe it.
- It condenses the rules by separating the alternatives with "|".
id_list_tail => , id id_list_tail | ;
- Kleene star or plus are used to denote repetition:
id_list => id ( , id) * ;
UN => (digit)+
- * means that the content of the parenthesis is repeated 0 or any number of times.
- + means that the content of the parenthesis is repeated one or more times.
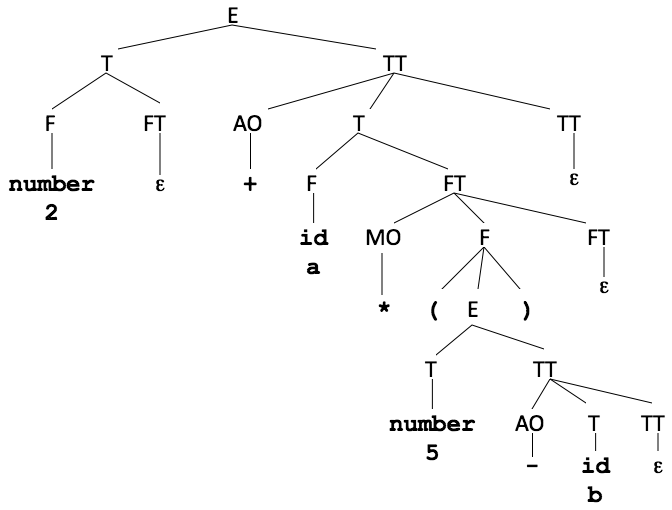
Arithmetic Expression
expr => term term_tail 1
term_tail => add_op term term_tail | e 2|3
term => factor factor_tail 4
factor_tail => mult_op factor factor_tail | e 5|6
factor => ( expr ) | id | number 7|8|9
add_op => + | - 10|11
mult_op => * | / 12|13
Discriminating Terminals
- expr : no need to check a terminal
- term_tail :
+ or - -> the first rule,
anything else -> the second
- term : one rule, no need to check
- factor_tail :
* or / -> the first rule
anything else -> the second
- factor :
( -> the first rule
id or number -> the two others
anything else -> error
- add_op, mult_op: +, -, *, / ok, anything else error
- This is LL(1).
Parsing Process
2 + a * ( 5 – b )
E ->T TT ->F FT TT -> (F 2) FT TT -> (F 2) TT ->
(F 2) AO T TT -> (F 2) (AO +) T TT -> (F 2) (AO +) F FT TT ->
(F 2) (AO +) (F a) FT TT -> (F 2) (AO +) (F a) MO F FT TT ->
(F 2) (AO +) (F a) (MO *) F FT TT ->
(F 2) (AO +) (F a) (MO *) (E) FT TT ->
(F 2) (AO +) (F a) (MO *) (T TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) (F FT TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) FT TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) TT) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) AO T TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) (AO -) T TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) (AO -) F FT TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) (AO -) (F b) FT TT ) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) (AO -) (F b) TT) FT TT ->
(F 2) (AO +) (F a) (MO *) ( (F 5) (AO -) (F b) )
Parse Tree