Blind Search
C463 / B551 Artificial Intelligence
Intelligent Agents
Problem Solving
- Problem-solving is the activity of finding sequences of action that will most likely lead to desirable states of the environment (solutions).
- Goal-driven agents usually do problem-solving.
- It requires a clear formulation of the goal.
- The goal is usually a condition to be satisfied by the state of the environment.
- The agents can be informed or uninformed based on the knowledge they have about how to search for the solution.
Problem Solving by Search
- Suppose an agent is in a given state and none of the possible actions it can take achieves the goal.
- Then the agent must explore the space of possible action sequences in search for the one leading to the goal.
- A search algorithm receives an input problem and returns a sequence of actions that leads to the solution.
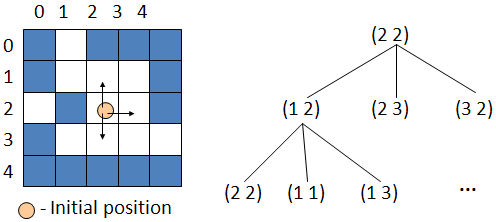
- Example: given a maze in 2D grid and an initial position, find a path in the maze that leads to an exit.
Problem Formulation
- Problem description:
- the environment (the maze itself)
- the initial state (location in the maze, (x y) )
- possible actions for the agent (move in 4 directions when the next cell of the maze in that direction is a space). The space of possible actions can be seen as a graph if the environment is deterministic.
- the goal test (are we there yet?)
- a path cost, that tells us if a path to the goal is better than another.
Search Tree
- A tree where each node is a possible state and the parent-child relation is defined by actions to be taken.
- The root of the tree is the initial state.
- From each node of the tree we can generate children by taking the possible actions from that state. This is called expanding the node.
- Many times the actual tree is implicit in the problem-solving algorithm.
Example
:
Move Up
(defun moveup (pos)
(let ((x (car pos)) (y (car (cdr pos))))
(if (> x 0) (list (- x 1) y) nil)))
def moveup(pos):
x = pos[0]
y = pos[1]
if x>0:
return [x-1,y]
else
return []
Uninformed Search Strategies
- Also called blind search.
- 2 major search strategies when we have no way to direct the search, taken from graph theory.
- Breadth-first search: builds the search tree by levels. It usually involves a queue of visited states. It will find the shallowest goal (closest to the root).
- Depth-first search: explores a path going down in the tree until it finds a solution or until it reaches a dead end. At that point it backtracks to search other paths. The easiest implementation is recursive.
Search Variations
- Uniform-cost search. When all steps don't have the same cost, at every point we can expand the node of the lowest path cost instead of the closest to the origin. Equivalent to the Dijkstra algorithm.
- Depth-limited search - expand nodes with DF until we reach a given depth in the tree.
- Iterative deepening DF - a depth limited search where the depth limit is incremented until we reach the goal. Combines DF and BF.
- Bidirectional search - run a search forward from the initial state and backward from the goal until they meet.
Search Performance
- Completeness - if there is a solution, will the algorithm find one?
- Optimality - does the algorithm find the optimal solution (defined in terms of some cost)?
- Complexity: time and space required.
- Consider b the branching factor (how many branches expand from every node), d the depth of the shallowest goal, and m the maximum length of any path in the search space (could be infinite).
Search Complexity
- Time complexity:
- BF - O(bd+1).
- DF - Best case, O(d). Worst case O(bm)
- Space complexity:
- BF - O(bd+1). We must store all generated nodes until we find the goal.
- DF - Best case O(d). Worst case O(m). We only need to store the current path. The space can be optimized if the actions are reversible.
Expanding - Search Lists
- In some cases the search can come back to a previously visited state which causes loops (possibly infinite).
- To avoid loops the search can keep track of the visited states.
- Expanding a node: adding its children to the search.
- Closed list: a list of all the expanded nodes.
- Open list: list of nodes that can be expanded next.

