Informed Search

Informed Search

• A search using domain-specific knowledge.
• Suppose that we have a way to estimate how close a state is to the goal, with an evaluation function.
• General strategy: expand the best state in the open list first. It's called a best-first search or ordered state-space search.
• In general the evaluation function is imprecise, which makes the method a heuristic (works well in most cases).
• The evaluation is often based on empirical observations.

Examples

• The vacuum cleaner - it might move from a cell towards the dirtiest adjacent cell.
• For a path-search in a graph with a geometrical representation - give preference to the neighbors which are the closest to the target based on the Euclidian distance (which may or may not be an indication of a good path). This is called a greedy search algorithm.
• For a game-playing, the algorithm may move to a state giving it a strategic advantage (capturing the opponent's queen).

Heuristic Examples

• Tic-Tac-Toe: the number of tupples (2 or 3) or pieces that are aligned.
• Jigsaw puzzle: the length of the completed border and the number of large continuous completed areas.
• The 8-Queens problem: the number of cells that are not yet attacked by any of the queens.
• For a maze: the Manhattan distance to the target
  row difference + column difference.

The A* Search

• A well known method that minimizes the estimated solution cost.
• Let g(n) be the cost of the path from the initial state to the current state n.
• Let h(n) be the estimated distance from the current state to the goal. This is a heuristic.
• The estimated cost of the cheapest solution through n is
  f(n) = g(n) + h(n)
• Given a good heuristic h, A* is both complete and optimal.
• The method is similar to the best-first where "best" is defined by the estimated cost f(n).

def A_star(initial):
   open_list = [initial]
   close_list = []
   goal = False
   while open_list and not goal:
      state = pop(open_list)
      if state in close_list: continue
      else: close_list.append(state)
      if (reach_goal(state)):
         goal = state
      else:
         children = expand-state(state)
         open_list += children
         open_list.sort(f_value)
   return goal

Small Example of Graph
 

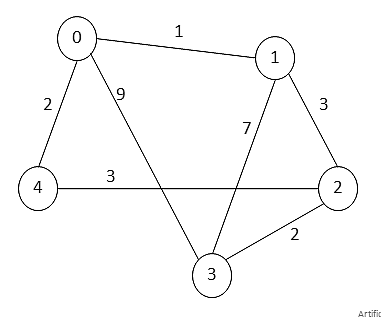
Admissible Heuristic

• A heuristic h is called admissible if it never overestimates the cost to reach the goal from a state. Which means that
  h(n) < Min( cost( path(n, goal)))
  over all paths leading from n to the goal.
• Search for a path in a geometric graph: the length of a path from vertex A to vertex B can never be less than the distance between A and B. So the actual distance is an admissible heuristic.

Consistent Heuristic

• A heuristic is consistent if for any n and c where c is a child state of n,
  h(n) < h(c) + cost( edge(n, c))
• This is known as the triangular inequality.

Optimality and Completeness

• A* with an admissible heuristic is optimal for a tree search, meaning when there is only one path to any given state.
• A* with a consistent heuristic is optimal for any kind of search (graph search), even if several paths can lead to the same state. In this case we must not exclude states we have seen before, but update their information when their information when the new path is better.
• A* is complete if the search graph is finite or when there is no infinite path in the graph having a finite total cost.

Example

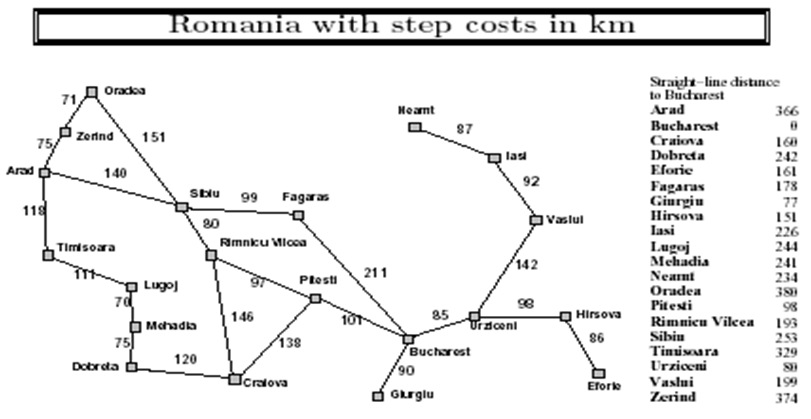
Starting from: timisoara. Goal: bucharest.

lugoj: g = 111, h = 244, f = 355
((lugoj 355) (arad, 484))
mehadia: g = 181, h = 241, f = 422
((mehadia 422) (arad 484))
((arad 484) (dobreta 498))
((dobreta 498) (sibiu 511) (zerind 567))
((sibiu 511) (craiova 525) (zerind 567))
((craiova 525) (rimnicu 531) (fagaras 535) (zerind 567))
((rimnicu 531) (fagaras 535) (zerind 567) (pitesti 611))
((pitesti 533) (fagaras 535) (zerind 567))
((fagaras 535) (bucharest 546) ((zerind 567))
((bucharest 546) (zerind 567) (bucharest 568))

Path: timisoara->arad->sibiu->rimnicu->pitesti->bucharest

Recursive Best-First Search (RBFS)

• An implementation of the depth-first using the estimated cost f and abandoning a path when its cost becomes too big.
• For every generated state it computes the f-value. The depth-first expands the current states in the order of the f-value.
• While expanding any state, the algorithm keeps track of the next smallest f-value of an alternative path. If the f-value of the best expanded state is larger than the best alternative path, then the current state is abandoned.

; Lisp version
(defun rbfs (state best-alt)
  (cond ((reach-goal state) state)
    ((not state) nil)
    (t (setq children (expand-state state)
             goal nil)
       (while (and children (not goal))
         (sort children f-value)
         (setq child (car children))
         (setq ba (f-value (cadr children)))
         (if (or (not ba) (< best-alt ba))
             (setq ba best-alt))
         (if ((> (f-value child best-alt)) 
                (setq children nil))
            ((setq goal (rbfs child ba)) 
                goal))))))

#Python version
def rbfs(state, best_alt):
   if not state or reach_goal(state): 
      return state
   else:
      children = expand_state(state)
      goal = False
      while not goal:
         children.sort(f_value_compare)
         child = children[0]
         if f_value(child) > f_value(state):
            f_value(state) = f_value(child)
         if f_value(child) > best_alt: 
            return False
         alt = best_alt
         if len(children) > 1 and f_value(children[1]) < best_alt:
            alt = f_value(children[1])
         goal = rbfs(child, alt)
      return goal
      

Iterative Deepening A* - IDA*

• Similar to the iteratively deepening search.
• The limit for expanding a state is not given by the depth but by the f-value.
• It starts with the limit being the f-value of the initial state.
• If the goal is not found, the limit is increased by a constant or to the lowest f-value found in the previous search that exceeds the previous limit, and the depth-first search restarts.
• It can require more time than A*, but they are asymptotically similar. IDA* needs a lot less memory.

; Lisp version
(defun ida* (state limit)
  (cond ((reach-goal state) state)
    ((not state) nil)
    (t (setq children 
             (sort (expand-state state) f-value)
             child (pop children) 
             goal nil)
       (while (and child (not goal))
         (cond ((> (f-value child limit)) 
                (setq child nil))
               ((setq goal (ida* child limit)) 
                 goal)
               (t (setq child 
                        (pop children))))))))

#Python version
def ida*(state, limit)
   if not state or reach-goal(state): 
      return state
   else: 
      children = expand_state(state)
      goal = False
      while not goal:
         children.sort(f_value_compare)
         child = children[0]
         if f_value(child) > f_value(state):
            f_value(state) = f_value(child)
         if f_value(child) > limit:
            return False
         goal = ida*(child, limit)
      return goal

Simplified Memory-Bounded A* - SMA*

• It's an A* that is allowed to generate only a fixed number of states at any moment.
• It proceeds like A* until it reaches the node limit.
• At that point it uses the f-value to eliminate the worst node from the search tree.
• If several nodes have the same worst f-value, it eliminates the oldest of them.
• SMA* is complete if the depth of the shallowest goal d is less than the available memory (number of nodes it can generate).

Pattern Databases

• A database of substates or patterns. For example, for the 8-tile puzzle, all the possible configurations for the tiles 1, 2, 3, 4.
• For every pattern, the database contains the estimated cost for it which is the minimal cost to the solution for any state that contains the pattern.
• The algorithm uses the pattern database to search for all the patterns that apply to a given state. The estimation for that state will be the maximum cost among all the patterns that apply.