Local Search
C463 / B551 Artificial Intelligence
Constraint Satisfaction Problem (CSP)
Constraint Satisfaction Problem (CSP)
- A constraint is a condition to be satisfied by a state. The goal is defined in terms of a set of constraints.
- Let the state space be described by a set of variables (x1, x2, ..., xn),
each of them taking values from a domain Di.
A state is an assignment of values to each of the variables xi.
- Constraint: a function (predicate) of these variables taking the values true or false.
- C(x1, x2, ..., xn) = true | false
- CSP - find any particular state such that a set of constraints {C1, C2, ... Cm} are satisfied.
Domains
- Boolean: {true, false} or {0,1} (binary).
- Finite: a limited number of possible values for each variable.
- Discrete: an enumerable set of values (first value, second, ...). A domain can be discrete but not finite,
like the set of integer numbers.
- Continuous: real numbers.
- A set of linear constraints on continuous domains can be solved in polynomial time by linear programming.
Constraints
- The constraints might not involve all of the variables.
- A unary constraint involves 1 variable.
- A binary constraint involves 2 variables.
- Several constraints could be expressed as a single one by combining them in a conjunctive statement (and C1 C2 ...).
- Sometimes we must find an entire path for which the constraints are satisfied. In this case the goal is defined by
either an extra constraint or an objective function to optimize.
- Sometimes the constraint are expressed as preferences.
Example
- The goat-wolf-cabbage problem (also known as the farmer - goose - fox - grain problem.
- State space: variables (G, W, C, M), each taking the values 0/1.
- Constraints:
C0: (G & W & C & M) // initial
C1: (! ((G & W & !M) | (!G & !W & M)))
C2: (! ((G & C & !M) | (!G & !C & M)))
C3: (!G & !W & !C & !M) // goal
- We want a path such that C1 & C2 are satisfied.
The initial state is expressed by C0 and the goal by C3.
Note that both C0 and C3 describe states that satisfy C1 and C2.
Incremental CSP
- Some problems can be solved by incrementally assigning values to the variables.
- Initial state: no assignment.
- Successor function: assigning a value to a previously unassigned variable if this does not cause a conflict with any of the constraints.
- Goal: when we successfully assigned a value to every variable.
- What if all the values we can assign the next variable generate conflicts? -> Backtracking.
Example
- Graph coloring problem: given a planar graph, assign one of 4 colors to each vertex such that any
two adjacent vertices have different colors.
- Canadian provinces: Alberta (AB), British Columbia (BC), Labrador (LB), Manitoba (MB), New Brunswick (NB),
Newfoundland (NF), Northwest Territories (NT), Nova Scotia (NS), Nunavut (NV), Ontario (ON), Prince Edward Island (PE),
Quebec (QC), Saskatchewan (SK) Yukon Territory (YT).
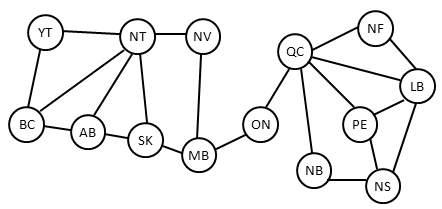
- Variables: AB, BC, ..., YT.
- Domains = {yellow, blue, red, green}.
- Constraints: BC != YT, BC != NT, etc.
Map
Constraint Graph
Cryptarithmetic Problems
Value Ordering
- In the successor function, the default value being chosen for the variable is the next one that hasn't yet been used.
- Which variable do we assign a value to next? How do we choose the value?
- This is usually based on a static ordering of the values and of the variables.
- A value that does not violate any constraint is called legal or consistent.
Choice Heuristics
- Minimum remaining values MRV: choose the variable from the list of unassigned that has the least number of possible values.
This reduces the size of the search tree.
- Degree heuristic: at every point choose the variable that is the most involved in constraints.
That will reduce the choices in the tree afterwards.
- Least constraining value: choose a value for the variable that eliminates the least
number of choices for the unassigned variables.
Information Propagation
- Forward checking: after assigning a value to a variable, the algorithm can look at all the unassigned
variables linked to it and eliminate from their domain the values that are in conflict with it.
- If any of these variable end up with an empty domain, then this is not a good value for the variable.
- Constraint propagation: propagating the implications of constraints in the graph to check for inconsistencies.
Arc Consistency
- An arc AB or constraint involving two variables A and B is consistent if for every value of the
variable A there exists a value for the variable B such that the constraint is satisfied.
- k-consistency: a constraint involving k variables is consistent if for every combination of values for
k-1 of these variables, there exists a value for the kth one such that the constraint is satisfied.
- If the constraints are expressed as a graph, then the k-consistency means that every path of length k-1 is k-consistent.
Backjumping
- An intelligent version of the backtracking.
- When the search forward fails, this method goes back not to the latest variable for which another value could be assigned, but to the variable that generated a conflict in the constraints.
- Conflict set: the set of all variables involved in conflicts.
- Backjumping: going back to the most recent variable in the conflict set.



