Local Search
C463 / B551 Artificial Intelligence
Adversarial Search
Adversarial Search
- In particular for games involving two opposing players that
attempt to achieve a mutually exclusive goal.
- It can have other applications (economics).
- They qualify as competitive multi-agent environments.
- The players take turns to make a move.
- The environment is strategic, often of perfect information.
Game Problem Setup
- Initial state - positions of every piece involved on both sides
and which player has the next move.
- Successor function - identifies the legal moves from any state
- Terminal test - knowing when one of the player won the game or
when there is a draw.
- Utility (payoff) function - an evaluation of the terminal states,
like the score.
- A heuristic estimating the payoff for an intermediate state is
also often used when the game tree is too large to compute completely.
Minmax
- A strategy assuming that each player is
choosing the next move to maximize their utility function.
- Minmax(state n):
- utility(n) if n is a terminal state
- max{ minmax( successor(n))} if n is a state where the current
player has the next move,
- min{ minmax( successor(n))} if n is a state where the opponent has
the next move.
Minmax
- The minmax algorithm with 1 level aims to maximize the utility or
estimated payoff of all the legal moves available to the player.
- For 2 levels, it assumes that the opponent will optimize their
payoff from the move after the next, so the player minimizes the
utility for the opponent. Each odd level in the tree minimizes its
descendants, while each even level maximizes them. If the tree is
very big, it may not be practical to expand it to the terminal
states. In that case we can choose a maximal expansion depth.
Example: Sticks Game
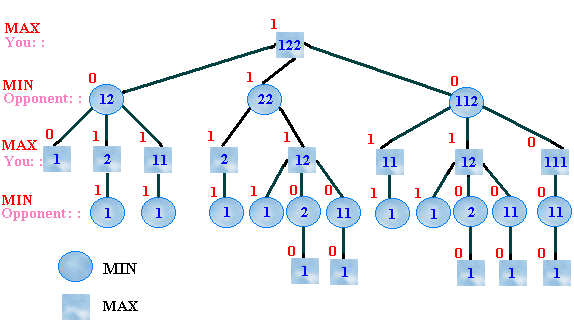
The players have piles of sticks. They can remove any number of sticks
from any one pile. The one removing the last stick loses.
Minmax Algorithm
; Lisp version
def minmax(n, what):
if n is a terminal node:
return its score
else:
compute the score of all of
its children using 1-what
if what == 1:
return the max score of the children
else:
return the min score of the children
# Python version
(defun minmax (n, what)
(if (terminalp n) (score n)
(let ((scores nil))
(dolist (s (expand n))
(push (cons s
(minmax s (- 1 what)))
scores))
(if (= what 1) (max scores)
(min scores)))))
Alpha-Beta
- Idea: pruning some of the subtrees once we know enough about them
to decide that they don't contribute to the decision for the next
move.
- It uses a global best move in the tree for each side (alpha = us,
beta = opponent).
- For alpha (us) the value starts with the -infinity and increases
over time as we find better moves.
- For beta (the opponent) the value starts as +infinity and
decreases over time as the opponent find moves that disadvantage us
better.
Alpha-Beta
- ALPHA value of a node
It is a value never greater than the true score of this
node. Initially it is the score of that node, if the node is a leaf,
otherwise it is -infinity. Then at a MAX node it is set to the largest
Beta score of its successors, and at a MIN node to the alpha value of
its predecessor.
- BETA value of a node
It is a value never smaller than the true score of this
node. Initially it is the score of that node, if the node is a leaf,
otherwise it is +infinity. Then at a MIN node it is set to the
smallest of the Alpha scores of its successors, and at a MAX node to
the beta value of its predecessor.
- For a terminal node alpha = beta = utility score.
Alpha-Beta for a MAX node
def MAX_AB (N, A, B):
if N is a leaf:
return its score;
else:
alpha = -infinity
for each successor S of N :
val = MIN_AB(S, max(A, alpha), B)
if val > alpha:
alpha = val
if alpha >= B: ]: #prune the subtree
return alpha
return alpha
Alpha-Beta for a MIN node
def MIN_AB (N, A, B):
if N is a leaf :
return its score
else :
beta = +infinity
for each successor S of N:
val = MAX_AB(S, A, min(B, beta))
if val < beta:
beta = val
if A >= beta: #prune the subtree
return beta
return beta
Example:
+infinity = 20, -infinity = -20
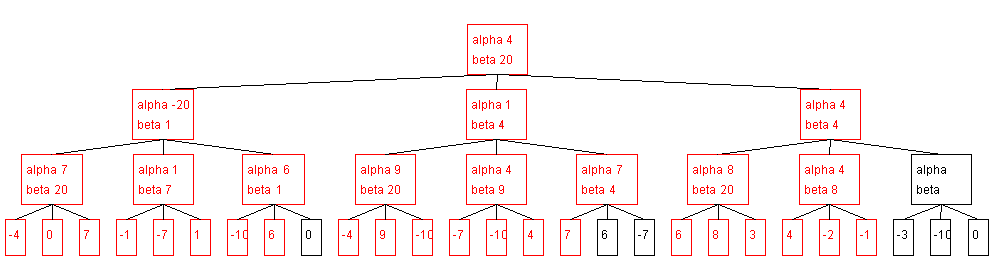
Pruning a min subtree
Applet:
http://www.ocf.berkeley.edu/~yosenl/extras/alphabeta/alphabeta.html
 ->
-> 
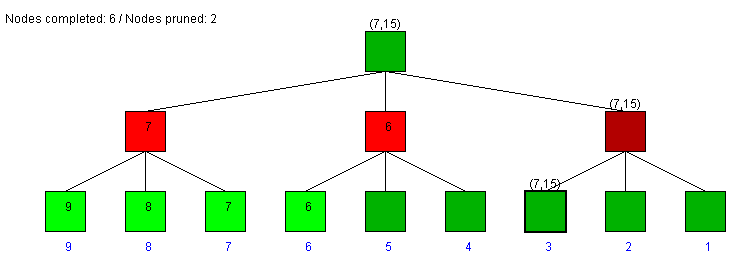
As 3 < 7, we know the opponent will choose something
equal or smaller, so we can discard the rest of the tree
because we already have a better move (7).
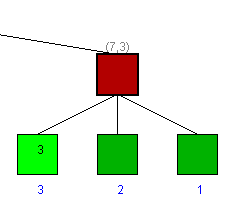
Pruning a max subtree
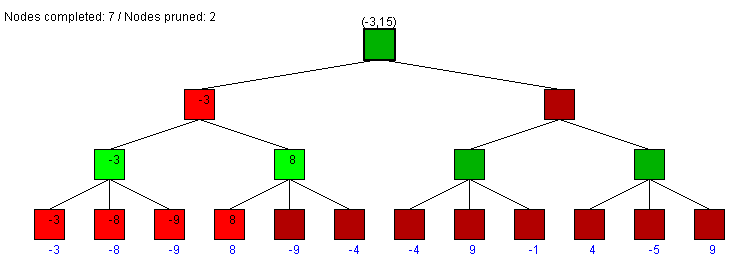
When we find 8 at the bottom, the parent was (-15, -3) and 8 replaces
-15. As 8 > -3 we update alpha of the parent (the red node above), and
it becomes (8, -3) before. Since that is the opponent, it will notice
that we got a better move and not give us a chance to take it. So the
opponent discards that node, which means that we don't have to
evaluate the rest of the subtree. Since this was the last green child
at this level, we can finalize the red node above with alpha = beta =
-3.
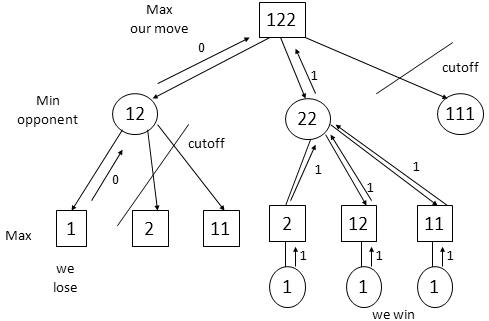
Cutoff Methods
- Sometimes we know a global minimum and maximum.
- If the value of beta reaches the global minimum, there's no use
searching forward.
- The same thing for alpha, if its value reaches the maximum, we can
prune the rest of the subtrees.
- For example, in a win-lose situation, when we find a path from
which we can win, there's no point looking at alternatives. We can
also assume that if the opponent finds a state where we lose, there's
no point looking for other states.
Cutoff
Games Involving Chance
- The successors of a state n can be a list of states depending on a
probabilistic event, like throwing a die, or drawing another card.
- Suppose the successors are {s1, s2, ... sk} where each of them can
occur with a probability pi, and resulting in an estimated score vi.
- Then the score returned by this node will be
score(n) = Sum ( pi * vi)
the sum of the individual scores weighted by their probabilities.
- Sometimes the probabilities are not completely known (card games)
and they are estimated.
Othello
- An 8x8 board. Each player has 32 pieces with one face white and
one black.
- A piece will capture (reverse) all the pieces of the opponent that
are on a line (including diagonal) between the new piece and another
one of the player's color.
- Only moves capturing at least one opponent piece are legal.
- The game ends when no more moves are possible.
- The player with the higher number of pieces wins.
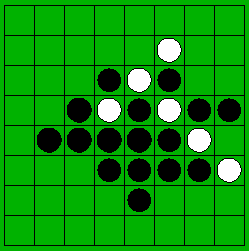
Legal Moves
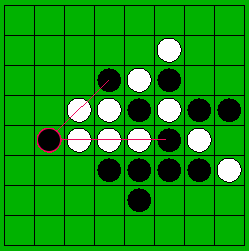 ->
-> 
Heuristic Payoff
- Tic-Tac-Toe: one could assign a value of 4 to the center,
of 2 to the corners and of 1 to the rest of the board.
- Othello:
- the number of captured pieces in one move
- corners are good
- squares next to corners are not good,
- borders are better than interior squares



 ->
-> 


 ->
-> 