Local Search
C463 / B551 Artificial Intelligence
Logic and Reasonning
Outline
- Logic and Reasoning
- Re-introduction to formal logic
- Reasoning, formal proof
- Knowledge representation
- Fuzzy logic, probabilistic reasoning
- Expert systems
Formal Logic
- Propositional logic, or Boolean, or zero degree. Uses only Boolean variables and operators.
- Predicate logic, or first degree. Predicate: a function of any variables taking Boolean values.
Uses quantifiers also (", $) attached to variables.
- Second degree logic: where the quantifiers can be attached to the predicates.
The predicates themselves become variables.
- Fuzzy logic: using a range of truth values instead of true/false, like [0, 1].
Propositional Logic
- Logic variables are called symbols (symbolic logic). They can be either true or false.
- A sentence or proposition is built using symbols and logic operations:
- not (!): !T = F, !F = T.
- and (conjunction, ^, &): T & T = T, anything else is F.
- or (disjunction, |): F | F = F, anything else is T.
- xor (exclusive or, x): T x F = F x T = T, anything else is F.
- implies (=>): T=>F = F, anything else is true. A =>B means that if A is true, then B must also be true.
- equivalent (<=>): T<=>T = T, F<=>F = T, anything else is F.
Truth Table
| A |
B |
A & B |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| |
| A |
B |
A => B |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
|
| A |
B |
C | -
(A x B) => C |
| T | T | T | T |
| T | T | F | T |
| T | F | T | T |
| T | F | F |
F |
| F | T | T | T |
| F | T | F |
F |
| F | F | T | T |
| F | F | F | T |
Proposition Evaluation
- For each assignment of values to the variables model, the entire proposition is evaluated to either true or false.
- Tautology: a proposition that is true for any assignment of values to the variables (example: A | !A). Also called valid.
- Contradiction: a proposition that is false for any assignment of values to the variables (example: A & !A)
- SAT: a proposition is satisfiable if there exists an assignment of values to the variables that make it true (example: A => B)
Problem Reduction
- To find out if a proposition is a tautology, we can find out if its opposite is a contradiction.
- We can find out if a proposition is a contradiction by the same algorithm as for SAT.
- If the answer to SAT is true, then the proposition is not a contradiction.
- If the answer to SAT is false, then the proposition is a contradiction.
- The 3 problems are equivalent and they are NP-complete.
Problem Reduction - HC
- Hamiltonian circuit: in a graph, find a cycle that passes through each vertex only once.
- We can denote each edge in the graph by a variable.
- Each vertex must have a single incoming edge and a single outgoing edge.
- This can be expressed by an xor over all the variables representing the edges.
HC Proposition Example
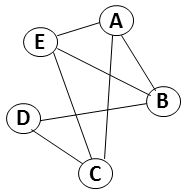
|
(and
(xor AE AC AB)
(xor EA CA BA)
(xor BA BE BD)
(xor AB EB DB)
(xor CA CE CD)
(xor AC EC DC)
(xor DC DB)
(xor CD BD)
(xor EA EB EC)
(xor AE BE CE)
)
|
Graph Coloring
- Each vertex can have one of the four colors {Y, R, B, G}. The condition is that two adjacent
vertices have different colors.
- We can expressed the fact that A has any of the 4 colors by a particular variable.
(AY  AR
AR  AB
AB  AG) ;
AG) ;
must have a single color; one and only one of these must be true.
- A has a different color that B:
(!(AY & BY) & !(AR & BR) & !(AB & BB) & !(AG & BG))
Reasoning
- A set of rules that allow us to deduce new propositions from the ones we already have.
- Deducing new propositions is called inference.
- A sequence of inferences is called a proof.
- A reasoning system is given a set of propositions known to be true (facts or hypotheses) and is asked if a
particular proposition (conclusion) can be deduced from them.
- If h1, h2, ... hn are the facts, and C the conclusion, then
(h1 & h2 & ... & hn)=> C
must be valid (a tautology).
Inference Rules
- Modus Ponens: from A and A=>B we can deduce B.
- And-elimination: from A & B we can deduce either A or B.
- Or-elimination: from A | B and !A we can deduce B.
- Or-addition: from A we can deduce (A | B).
- De Morgan rules: !(A & B) is equivalent to (!A | !B) and the other way around.
- Contrapositive: A=>B is equivalent to !B =>!A.
- Implication: A=>B is equivalent to !A | B.
Conjunctive Normal Form
- A variable or its negation is called a literal – positive or negative : A, !B,
- A clause is a disjunction of literals
A | !B | !C | D.
- A proposition is in conjunctive normal form if it's expressed as a conjunction of clauses:
(A | B) & (!A | B | D) & (A | !B | !C | D).
- Theorem: every proposition using the logical operators introduced before can be expressed in conjunctive normal form.
Examples
- x
 y ~ (x & !y) | (!x & y) ~ (x | y) & (!x | !y)
y ~ (x & !y) | (!x & y) ~ (x | y) & (!x | !y)
- Distributive law:
- a & (b | c) ~ (a & b) | (a & c)
- a | (b & c) ~ (a | b) & (a | c)
- Bring to CNF: (a & b) => (!b | c)
(x => (y & r)) => (y | (!x & r))
- Reasoning: If the unicorn is mythical, then it is immortal, but if it's not mythical, then it is a mortal mammal. If the unicorn is either immortal or a mammal, then it is horned. The unicorn is magical if it is horned.
Resolution Algorithm for SAT
- Clause resolution. Suppose we have the following clauses: (a | b) and (!a | c)
- These two clauses are satisfiable if either b or c is satisfiable. Thus we can replace them with the clause (b | c) or simply add it.
- If we obtain a clause containing two opposite literals, we can eliminate it: (b | !b | ...) is always satisfiable.
- If we end up with an empty clause, we have a contradiction.
- If we end up with an empty set of clauses, then the original proposition was satisfiable.
Automatic Proofs
- Suppose we have a collection of propositions that describe the facts in our database, like KB.
- We would like to prove some new fact a.
- This means that we must prove that KB =>a is true (valid), or that (!KB |
a) is true.
- We can negate the formula above and obtain (KB & !a).
- If this formula is a contradiction, then the original implication is true. If the formula is satisfiable, then the original deduction cannot be made.
- We can use CNFs and the resolution algorithm.
Davis-Putnam Algorithm
- Early termination: if any clause is false, then the whole formula is false. If part of a clause is true, then the whole clause is true. A true clause can be eliminated.
- Pure symbol. A symbol appearing only as positive or only as negative is called pure. All the clauses containing it can be eliminated.
- Unit clauses. A clause composed of a single symbol will generate a value for that symbol.
- Unit propagation. A symbol that is false can be eliminated from a clause. This can cause other clauses to become units.
Davis-Putnam Examples
- Early termination: if somehow we know that A is true, then (A | B) & (A | C) is true.
- Also if A and B are false, then (A|B) & (A|C) is false.
- Pure symbol. (A | B) & (!B | D) & (A | C | !D). A appears only as positive, so we reduce this proposition to (!B | D).
- Unit clause: A & (B | C | !D) & !C & (A | D)
- A is a unit => A must be true =>(A | D) can be eliminated => result (B | C | !D) & !C
- !C is a negative unit => C must be false and we can eliminate it from (B | C | D) => result (B | !D).
Predicate (First Order) Logic
- Predicate: a function of any variables taking Boolean values (true/false).
- The predicate logic deals with logic formulas involving predicates, plus the quantifiers " (for all), $ (there exists).
- The formulas can involve variables, constants, expressions.
- The variables represent objects, the predicates are usually properties or relations, and the logic formulas represent known facts or rules.
- A variable is called bound if a quantifier applies to it. It is free otherwise.
Model
- Domain: the set of objects that the variables take values from.
- Model: a domain and any set of relations defined between the objects.
- Symbols: constants, functions, predicates.
- Interpretation: a particular meaning specified for each of the symbols.
- A formula is valid if it is true for every possible model and every possible interpretation.
Formal Definition
- Term: a constant, a variable, or a function of other terms.
- Atomic sentence: a predicate of some terms.
- Sentence: atomic sentence
(sentence and/or sentence)
!sentence
"/$ sentence
Quantifiers
- A sentence
 x P(x) is true if P(x) is true for all possible interpretations for x.
x P(x) is true if P(x) is true for all possible interpretations for x.
- A sentence
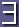 x P(x) is true if P(x) is true for at least one possible interpretation for x.
x P(x) is true if P(x) is true for at least one possible interpretation for x.
- The two quantifiers are not interchangeable:
 x
x 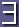 y P(x, y) !=
y P(x, y) != 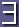 y
y  x P(x, y)
x P(x, y)
- The negation transforms one into the other:
!( x P(x)) ~
x P(x)) ~ 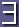 x !P(x)
x !P(x)
!(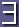 x P(x)) ~
x P(x)) ~  x !P(x)
x !P(x)
Validity
- A variable is called free in some context if no quantifier is attached to it.
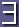 x (P(x) & Q(x, y)) x – bound, y – free.
x (P(x) & Q(x, y)) x – bound, y – free.
- Bound variables (not free) can be renamed as long as the new name doesn't appear elsewhere:
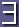 x P(x) ~
x P(x) ~ 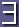 y P(y)
y P(y)
- A formula is valid (tautology) if its completion with a
 for every free variable is true.
for every free variable is true.
 y
y 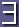 x (P(x) & Q(x, y))
x (P(x) & Q(x, y))
- The formula is satisfiable if its completion with a
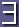 for every free variable is true.
for every free variable is true.
Example: Graph Coloring
(same graph as above)
- Domain: {A, B, C, D, E}
- Relation (edge): {{A, B}, {A, C}, ...}
- Model: domain + relation
- Function: color(x)
- Predicate: edge(x, y)
- Two adjacent vertices must not have the same color:
edge(x, y) => !equal (color(x), color(y))
- Graph coloring problem:
 x
x  y ( edge(x, y) => !equal (color(x), color(y)))
y ( edge(x, y) => !equal (color(x), color(y)))
A Problem
- Kayla's family consists of Daniel, Morgan, Grace, and Devin. They are Kayla's mother, father, younger brother, and younger sister.
- Name which person is the mother, father, younger brother, and younger sister.
- Daniel has no sisters.
- Daniel likes to jog. He jogs every morning.
- Morgan is not Kayla's mother. She is also not Kayla's father.
- Grace is not Kayla's younger brother.
Representation
- Domain: {kayla, daniel, morgan, grace, devin}.
 x (Equal(x, kayla)
x (Equal(x, kayla)  Mother(x, kayla)
Mother(x, kayla)  Father(x, kayla)
Father(x, kayla)  Brother(x, kayla)
Brother(x, kayla)  Sister(x, kayla) )
Sister(x, kayla) )
 x ! Sister(x, daniel)
x ! Sister(x, daniel)
- Like(daniel, jog) &
 d
d 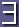 t (Morning(t, d) & Do(daniel, jog, t))
t (Morning(t, d) & Do(daniel, jog, t))
- !Mother(morgan, kayla) & !Father(morgan, kayla)
- !Brother(grace, kayla)
Additional Facts
- Female(kayla), Female(morgan), Female(grace), Male(daniel), Male(devin).
- Brother(x, y) <=> Sibling(x, y) & Male(x)
- Sister(x, y) <=> Sibling(x, y) & Female(x)
- Sibling(x, y) <=> Sibling(y, x)
- Mother(x, y) <=> Parent(x, y) & Female(x)
- Father(x, y) <=> Parent(x, y) & Male(x)
 x (Male(x) Ä Female(x))
x (Male(x) Ä Female(x))
 x, y, z ((!equal(x, y) & Mother(x, z)) => !Mother(y, z))
x, y, z ((!equal(x, y) & Mother(x, z)) => !Mother(y, z))
Horn Clauses
- A Horn clause is a clause where at most one literal is positive.
- They are obtained from implications:
(a & b & c) => d ~ (!a | !b | !c | d)
- It is a common thing when representing knowledge to describe rules as several known facts implying a new one.
- The resolution algorithm for Horn clauses is polynomial.
- Logic programming (Prolog):
d :- a, b, c;
Prolog Example
- factorial(0, 1). ;; fact
- factorial(1, X) :- equal(X, 1). ;; rule
- factorial(N, X) :- factorial(N-1, Y), equal(X, N*Y).
- The database enumerates all the facts and rules we describe when a predicate is true.
- Interrogating the database: it will go through all the clauses in order until one of them is true. If none of them is true, it returns false.
- factorial(3, 6) returns true.
- factorial(2, 5) returns false.
- factorial(2, X) returns all possible values for X that satisfy the predicate. In this case it will say true, and X = 2.
Reasoning in Predicate Logic
- Universal instantiation: from
 x S(x) where S is a sentence, we can deduce S(a) where a is any expression that evaluates to a constant. S(a) is the sentence where every occurrence of x has been substituted by a, denoted {x/a}.
x S(x) where S is a sentence, we can deduce S(a) where a is any expression that evaluates to a constant. S(a) is the sentence where every occurrence of x has been substituted by a, denoted {x/a}.
- Existential instantiation: we can replace
 x S(x) with S(k) where k is a constant that does not appear anywhere else in the KB. This k is called a Skolem constant.
x S(x) with S(k) where k is a constant that does not appear anywhere else in the KB. This k is called a Skolem constant.
- Basically a predicate logic sentence can be reduced to a propositional logic sentence and then the same inference rules can be applied.
- Generalized Modus Ponens
- If x is a variable (or a group of variables), P(x) is a sentence, and a is a constant (or group of constants) then from P(a) (substituting x by a) and
 x (P(x) => Q(x))
x (P(x) => Q(x))
we can deduce Q(a).
- Example: All humans are mortal. Socrates is human. Thus Socrates is mortal:
 x (Human(x) => Mortal(x))
x (Human(x) => Mortal(x))
Human(socrates)
- we can deduce Mortal(socrates).
Unification
- Finding a substitution for one or more variables with constants that makes two sentences look identical.
- Example: Sibling(x, kayla)
- Suppose that we have in the KB:
- Sibling(devin, kayla) and Sibling(morgan, kayla)
- Then there are two possible unifications that can be done of the first sentence with sentences from the KB: the substitution x = devin and x = morgan, or {x/devin} and {x/morgan}.
- Unification can also be called pattern matching.
Chaining
- The forward chaining starts from the known fact and makes deductions until it encounters the desired conclusion.
- The backward chaining starts from the conclusion or query and tries to find a sequence of inferences that proves it.
- The algorithm starts with a set of goals containing the query. It looks for all the substitutions of the current set of goals with the KB and adds any facts from which they can be derived to the set of goals, then calls itself recursively until the set of goals is empty.

