C481 B581 Computer Graphics
Dana Vrajitoru

2D Transformations

Definition. A function F that maps each point (x0, y0) from an original area to a point (x, y) = F(x0, y0) in the transformed area. In general T is a function with 2 components, (Fx, Fy).

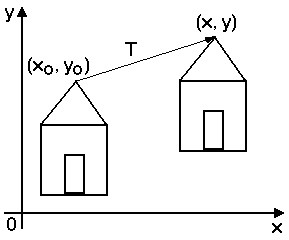
Direct computation:
for each (x0, y0) {
  getPixel(x0, y0, color);
  (x, y) = F(x0, y0);
  setPixel(x, y, color);
}

Drawback: although transformations are continuous functions in the real plane, when applied to a discrete area of pixels,  they may create gaps in the transformed area because of the scan conversion.

General method: apply the inverse transformation.

determine the boundary of the transformed area by a direct transformation;
for each (x, y) {
  (x0, y0) = F-1(x, y);
  getPixel(x0, y0, color);
  setPixel(x, y, color);
}

By this method, we leave no pixel out of the transformed area.


Translation of vector T(xt, yt):
Direct transformation
(
x
y
) = (
xo
yo
 ) + (
xt
yt		 )
Inverse transformation
(
xo
yo
) = (
x
y
 ) - (
xt
yt		 )


Rotation about the origin with an angle a:

Rotation matrix:

Ra
=(
cos a
sin a
 - sin a
 cos a		 ) 

Rotation as Change of Coordinates

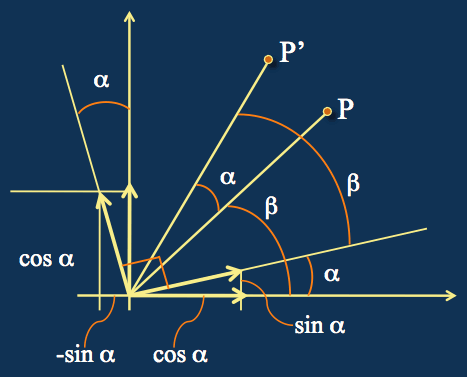
The point P' has coordinates in the frame of reference defined by the rotated unit vectors that are identical to the original coordinates of P in the frame Oxy. The two unit vectors are defined as v1 (cos a, sin a) and v2 (-sin a, cos a). To calculate the coordinates of P' in the frame Oxy, we need to multiply its coordinates in the frame (v1, v2) by the inverse of the matrix composed of the two vectors. This results in the rotation matrix described above.

Direct transformation
(
x
y
) =
 Ra * (
xo
yo		 )
Inverse transformation
(
xo
yo
) =
 R -a * (
x
y
 )

 
(
xo
yo
) = (
cos (-a)
sin (-a)
 - sin (-a)
 cos (-a)		 ) * (
x
y		 )
(
xo
yo
) = (
cos a
- sin a
 sin a
 cos a		 ) * (
x
y		 )


Scaling of factors a and b:

a = 1.7,   b = 0.8
Direct transformation
(
x
y
) = (
 a   0
0   b 		) * (
xo
yo
 )
Inverse transformation
(
xo
yo
) = (
 1/a   0
0     1/b 		) * (
x
y
 )


Symmetry (reflection) with respect to an axis:

Symmetry with respect to Ox
Flip vertically (axis = Ox)
 (
xo
yo
) = (
 1   0
0   -1 		) * (
x
y
 )

 
Flip horizontally (axis = Oy)
 (
xo
yo
) = (
 -1   0
0    1 		) * (
x
y
 )

Fractals

Def. Shapes that show similar features at different sizes.

From the programmer's point of view: recursively defined drawings.

Mandelbrot set:

Examples:
 
 
The Koch curve:
 The Sierpinski triangle

The Mandelbrot Set The Julia Set