Ray Tacing

C481 B581 Computer Graphics
Dana Vrajitoru

Ray Tracing

Global illumination model.
Consider the color of each pixel in the projected image as being determined by a ray of light arriving on this point according to the projection rule.

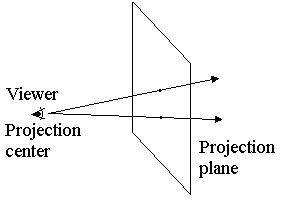
The Method

Send a ray from each pixel to the reverse direction of the light coming in.
Compute the closest intersection of this ray with any object.
Consider the ray in the direction of each light source from the intersection point (shadow rays).
For each of them, check if the ray intersects another object or not. Compute the local contribution from the rays without intersection.
Add to this the light obtained by reflection and refraction in this point computed recursively.

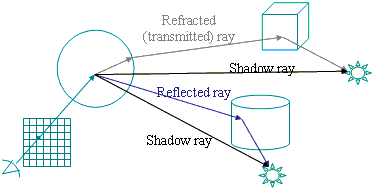
Recursive Reflection and Refraction

Determine the reflected and refracted (transmitted) rays from the current position based on the normal to the surface and on the specular and transparency properties of the surface.
Apply the algorithm recursively for each of these two rays.
Stop when reaching a source of light.
Stop when the ray doesn't intersect any other objects. In this case, add some background color.
The final color in the pixel adds the light from all the resulting rays.
The recursion can go for a limited number of steps.

The algorithm
color trace(point p, vector d) { //page 658 in the textbook
color local, reflected, transmitted;
point q; vector n;
q = intersection(p, d, status);
if (status == light_source)
return light_source_color;
if (status == no_intersection)
return background_color;
n = normal(q);
r = reflect(q, n); t = transmit(q, n);
local = phong(q, n, r);
reflected = trace(q, r);
transmitted = trace(q, t);
return (local + reflected + transmitted);
}

The Ray
A ray is given by a starting point (x₀, y₀, z₀) and a unit vector (x_d, y_d, z_d).
A point on the ray is defined by:
x = x₀ + t x_d
y = y₀ + t y_d
z = z₀ + t z_d
where t > 0.

The intersection between the ray and any surface S is given by the condition:
there exists t such that (x, y, z) is on S.
The problem of the intersection is in general complex.

Intersection with a Box

A box is given by the equations x_min < x < x_max, y_min < y < y_max, z_min < z < z_max.
The condition for the ray to intersect the box is
xmin < x₀ + t x_d < x_max and the same for y and z.
This gives us a system of 6 equations in t. If the intersection of their sets of solutions is not empty, then the ray crosses the box.
In general, defining a bounding box for every object can reduce the computations.

Intersection with a Sphere
A sphere is defined by a center (x_c, y_c, z_c) and a radius r. Then the distance between the center of the sphere and the point on the ray is
d²(t) = (x₀ + t x_d - x_c)² +(y₀ + t y_d - y_c)² +(z₀ + t z_d - z_c)² = a t² + b t + c
The minimum of this equation is obtained for t_min = -b/(2a) and the value is d_min = d(t_min)
If d_min <= r, then the ray crosses the sphere.
To compute the intersection, we must solve the equation d²(t) = r² .

Agent-Based RT

Divide the scene in volumes (can use octrees).
A different agent is responsible for each voxel.
The agent computes the intersection of any ray with objects belonging to that region.
When the ray leaves its region, the agent activates another agent.
Can be done in parallel.

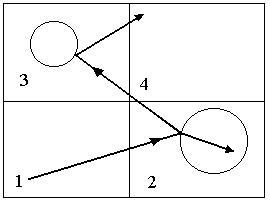
Ray Supersampling

Divide each pixel in several regions.
Compute the value for each region.
Average these values.
The subpixels can be chosen randomly according to a fairly even distribution.

Links:
POV Ray
http://www.siggraph.org/education/materials/HyperGraph/raytrace/rtrace0.htm
Internet ray tracing competition.
http://www.youtube.com/watch?v=XVZDH15TRro
http://www.youtube.com/watch?v=mtHDSG2wNho

Photon mapping
http://www.youtube.com/watch?v=ReI7AsF3nnE
http://www.youtube.com/watch?v=uwDu_q212SY