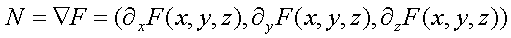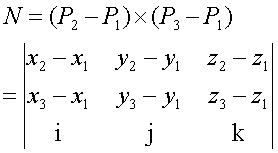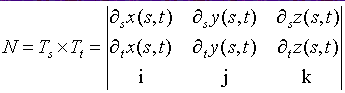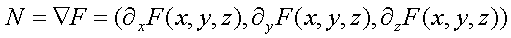C481 B581 Computer Graphics
Dana Vrajitoru
The Phong Model (cont)
Distance Term in the Phong Model
-
To include a term depending on the distance to the light source, if we
denote by
-
d = d (light source, Q)
-
I = kaIa + factor (kdId + ksIs)
-
where factor = 1/(a+bd + cd2)
-
The factor is know as the quadric attenuation term (see chapter 6 in the
textbook).
The Angle Between 2 Vectors
-
For 2 vectors A=(xa, ya, za), B =(xb,
yb, zb), by definition, their scalar product is:
-
AB = xaxb+ yayb+ zazb
=|A| |B| cos (A, B)
-
If |A|=1, |B|=1, we can compute the cosine of the angle between the 2 vectors
as:
-
cos (A, B) = AB = xaxb+ yayb+
zazb.
The Normal Vector
Computing the Normal Vector
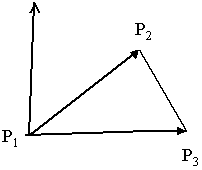
For a triangle defined by P1(x1, y1,
z1), P2(x2, y2, z2),
and P3(x3, y3, z3), and i=(1,0,0),
j=(0,1,0), k=(0,0,1):
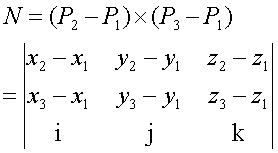
Normals for a Triangle Strip
-
The orientation of N depends on the order in which we multiply the vectors.
-
For a triangle strip, we must insure that the normals are consistently
oriented.
-
If P1, P2, P3, and P4 are 4
points of the triangle strip in sequence, then we compute
-
N1 = P1P2 x P1P3
-
N2 = P2P4 x P2P3
= P1+1P3+1 x P1+1P2+1
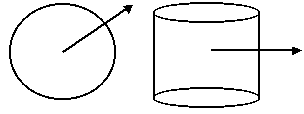
Examples of the Normal Vector
-
For a sphere centered in O, the normal to the surface in the point Q is
OQ.
-
For a cylinder around the z axis, the normal in the point Q=(x, y, z) is
N=(x, y, 0).
-
For any parameteric curve C(x(s), y(s), z(s)),
-
T = (x'(s), y'(s), z'(s)) is tangent to the curve, and
-
N = (x"(s), y"(s), z"(s)) is perpendicular to the curve.
Normal for a Parametric Surface
-
For a parameteric surface S(x(s, t), y(s, t), z(s, t)),
-
Ts = (¶s x(s, t),
¶s
y(s, t), ¶s z(s, t)) is tangent
to the surface,
-
Tt = (¶t x(s, t),
¶t
y(s, t), ¶t z(s, t)) is another
tangent to the surface,
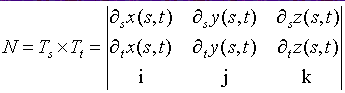
Normal for an Implicit Surface
For any surface defined implicitly by F(x, y, z) = c (constant), we
can compute the normal to this surface using the gradient of the function
F:
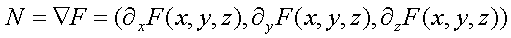
For a sphere: F(x, y, z) = x2 + y2 + z2
= 1
The gradient of the function is (2x, 2y, 2z). If we normalize it, we
obtain (x, y, z).