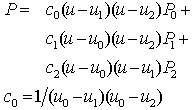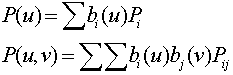C481 B581 Computer Graphics
Dana Vrajitoru
Representation and Modeling (continued)
Triangulation
Def. Given a set of points or vertices V={v1, v2,
..., vn}, find a set of triangles T={t1, t2,
..., tm} such as:
-
each triangle from T is based on vertices from V,
-
for each triangle, no other point from V apart from its vertices can be
found inside it,
-
the triangles form a convex surface containing all the points in V
-
triangle interiors do not intersect.
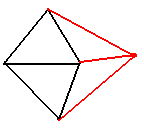
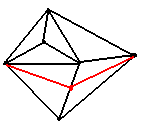
Example.
Lazy algorithm:
-
Start with an arbitrary point.
-
Find its two nearest neighbors.
-
Add one point at a time.
-
For each new point, add the triangles required for the surface to remain
convex.
Open and interesting problems
-
Finding an optimal triangulation for a given object in polynomial time,
that minimizes the number of triangles, the total edge length, or the total
surface area.
-
For OpenGL: finding a minimal number of triangle strips covering the object.
-
Resolution problems: reducing the number of triangle without losing details.
-
Related problems: convex boundary for a given number of points, polygonal
or circular (spherical).
-
Object morphing: computing the number of flips required to convert one
planar triangulation into another.
-
Fast remeshing after a local change.
Binary Space Partitioning Trees
A BSP tree is a recursive sub-division of space that treats each
line segment (or polygon, in 3D) as a cutting plane which is used to
categorize all remaining objects in the space as either being in
"front" or in "back" of that plane.
It has applications in hidden surface removal and ray tracing.
Example
Quadtrees and Octrees
Def. Multi-resolution representation in 2D (quadtrees) or 3D (octrees).
General idea: recursively divide the space into 4 square cells
(2D) or 8 cubic cells (3D) of equal size. 3D cells are also called voxels.
Each of them is either empty or full (belongs to the object or not). Divide
the size of the cell by 2 at each step.
Applications: medical imaging, fluid modeling, etc.
Examples:
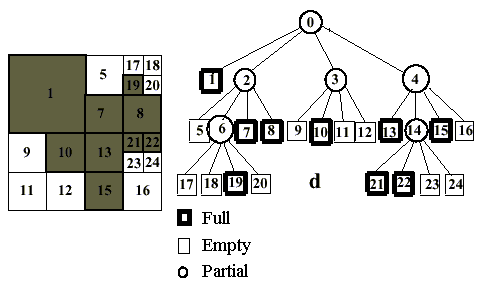
Quadtree
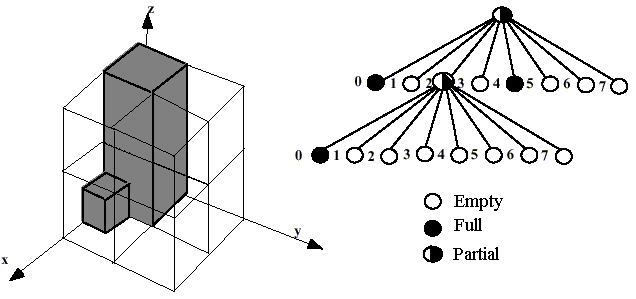
Octree
Metaballs (Blobs)
Each voxel is a ball. If two balls are close enough, they merge like drops
of water.
Used for modeling fluffy objects, fluids, animated characters, etc.
More information and examples:
Etheral3D
SIGGRAPH
metaballs page.
Interpolation Surfaces
Interpolating Curves
-
Simplest case: given a list of points P0, P1, P2, ..., draw a curve
that passes through each of them in this order.
-
Usually this is done by a polynomial function of degree the nr of points
-1.
-
We can also interpolate on subsets of points and add the resulting curves
(page 485-488).
-
We can also impose the continuity of the derivative up to a certain point
to insure the smoothness of the curve (page 493).
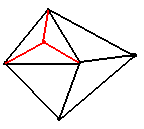
Interpolation on 3 Points

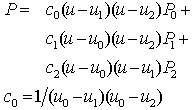
Bezier Curves
Some of the control points are used to define the tangent to the curve
(page 494).
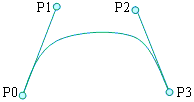
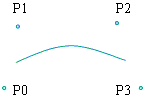
Spline Curves
-
Curves with continuity of the second derivative (curvature) with local
computations. The polynomial function is usually cubic.
-
Each curve segment is defined by 4 control points, none of which is actually
on the curve itself.
-
B-splines: bi-cubic.
Surfaces
-
Any interpolation type can be extended to surfaces by adding a second parameter
(v or t).
-
The best known are the NURBS surfaces (nonuniform rational B-spline).
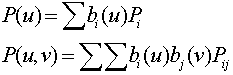
Nurbs in OpenGL
GLUnurbsObj *nobj;
nobj = gluNewNurbsRendered();
gluBeginSurface(nobj);
gluNurbsSurface(nobj, nrku, uknots, nrkv, vknots, du, dv, points,
4, 4, surf_type);
gluEndSurface(nobj);
// type: GLU_MAP2_VERTEX_3
Constructive Solid Geometry
The scene can also be represented as a tree, but the container nodes define
logical operations on the subtrees:
-
union (merge)
-
intersection
-
difference